SEAN MOBBERLEY

/ThreeMaterialDecomposition

Material decomposition is a technique that can be incorporated into MRI, X-ray and CT radiography to improve the isolation of tissues and materials (e.g. blood, fat, tissue or bone) within an image dataset. This improved differentiation of difficult-to-analyze anatomical areas is of particular importance in special diagnosis or prior to surgery. For example, the technique can be utilized to improve aneurism visualization, and in my functional pulmonary imaging lab, we used it to determine regional perfusion and ventilation heterogeneity to assess lung function.

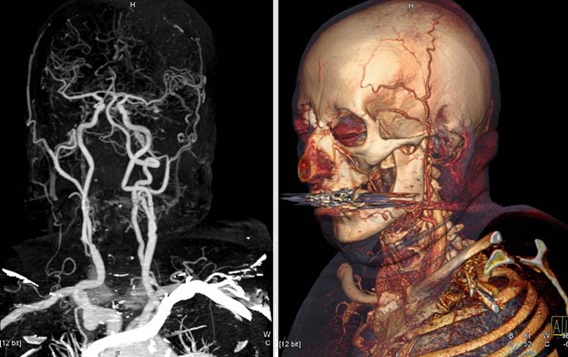
A 3-material decomposition is essentially a fanciful term for determining the elemental composition and mass fractioning within a region. It takes advantage of some x-ray attenuation properties at different energies (in CT) or atomic spin characteristics (in MRI). It also uses the conservation of mass and assumes that there are only two or three types of materials within a given voxel or homogenized volume and they can be differentiable under controlled acquisition settings.

I am not going to go into the X-ray attenuation physics behind the phenomenon here – if you are interested in that, you are welcome to read my thesis. What I will cover here is how you can actually perform a 3-material decomposition for yourself, using an ITK/C++ code similar to what I provide later on this page, as well as the fundamental theory and mathematics behind the technique.

Since my research has focused on using Dual-Source Dual-Energy (DSDE) CT in the pulmonary imaging field, my examples will come mostly from that area, however the same principles may hold true in other fields.

In chest CT imaging, if we consider the that the lung is composed of two materials -- e.g. “tissue” (including blood) corresponds with a CT number (intensity) of 50 HU and air has a CT number of -1000 HU -- then, using the conservation of mass, the fraction of HU density related to “tissue” and air within a volume can be can be calculated for each voxel in a region of interest.

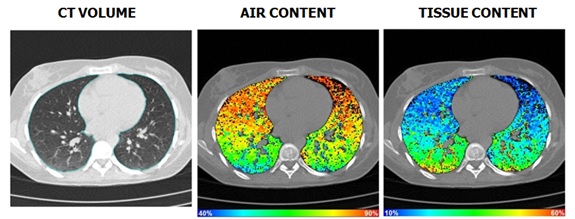
Total lung volumes are determined by the summation of segmented voxels in each slice, multiplied by conversion factors, based on slice thickness and image field of view, to produce perceptible results. By combining the total lung volume with tissue or air fractions, the absolute volumes of these materials in the lung are determined.

In any single projection measurement, we can only isolate two materials, e.g. water and air. However, using two energy beams, and exploiting known attenuation properties, a three-material decomposition can be performed. This allows us to effectively perform two scans in one and isolate contrast materials, with one radiation exposure and near perfect slice overlap, which is beneficial in the clinical environment where patient movement and radiation dose are a concern. In essence, dual-energy imaging works by imaging the same space in a single exposure, at two separate energies, e.g. one at 80 or 100 kVp and the other at 140 kVp, and deriving two separate attenuation measures to better understand the composition of an object.

Analogous to two-material decomposition, three-material decomposition can be performed using the conservation of mass assumption, i.e. the sum of the three mass fractions is equivalent to the mass of the whole mixture. Using this assumption, we can construct three simplified fundamental equations similar to our two material decomposition equation:

where and represents values acquired from scans at different energies, e.g. 80 kVp and 140 kVp. And contrast is typically iodine due to its stronger enhancement at low tube voltage settings, in addition to its physiologic properties.

Using these three equations, we can therefore derive the following matrix to determine the fractional content of the materials inside a voxel or object:

in practice, this allows for an isolation of contrast material in a volume. In addition to the isolation of contrast medium, by taking the weighted sum of images acquired at separate energies, and subtracting the image containing just the contrast enhancement, you effectively produces both a perfectly registered contrast enhanced image, and a “virtual non-contrast” (VNC) image derived from a single exposure.

Although the three-materials mentioned herein were for air, tissue, and contrast, any three materials can feasibly be isolated. For example, in liver parenchyma we can isolate fat, soft tissue, and iodine. By deducing that the stronger image enhancement at 80 kVp in relation to that of 140 kVp in an 80 kVp / 140 kVp DSDE scan is attributed to a certain concentration of iodine, we can perform a weighted and smoothed image subtraction to map the iodine content within the image. This same methodology can be used to easily remove any contrast material in image space, and can also be used to remove bone, as calcium has a relatively high Z. It is theoretically possible to discriminate between types of body tissue (e.g. vascular, scar, cancerous and muscle tissues) without the use of a contrast agent, however, since these tissues have a similar composition of basic biological atoms (carbon, hydrogen, oxygen, and nitrogen) which each demonstrate very similar X-ray attenuation characteristics at different energies due to their similar atomic numbers (Z ranges from 1-8), any differentiation of soft tissues without the use of contrast has proved to be a challenge.

For anyone interested, I have included here the stripped code that I use to perform a material decomposition, given two registered DICOM image datasets at different scan energies.

materialDecomposition.cxx:

#include "itkImage.h"
#include "itkImageFileReader.h"
#include "itkImageSeriesReader.h"
#include "itkImageFileWriter.h"
#include "itkRescaleIntensityImageFilter.h"
#include "itkSubtractImageFilter.h"
#include "itkGDCMImageIO.h"
#include "itkGDCMSeriesFileNames.h"

int main( int argc, char* argv[] )
{
	//Define file names
	if( argc < 4 )
	{
		std::cerr << "Usage: " << std::endl;
		std::cerr << argv[0] << " DicomDirectory outputFileName sigma [seriesName] "
		<< std::endl;
		return EXIT_FAILURE;
	}

	typedef signed short PixelType;
	const unsigned int Dimension = 3;

	typedef itk::Image< PixelType, Dimension > ImageType;

	typedef itk::ImageSeriesReader< ImageType > ReaderType;
	ReaderType::Pointer reader = ReaderType::New();

	typedef itk::GDCMImageIO ImageIOType;
	ImageIOType::Pointer dicomIO = ImageIOType::New();

	reader->SetImageIO( dicomIO );

	typedef itk::GDCMSeriesFileNames NamesGeneratorType;
	NamesGeneratorType::Pointer nameGenerator = NamesGeneratorType::New();

	nameGenerator->SetUseSeriesDetails( true );
	nameGenerator->AddSeriesRestriction("0008|0021");

	nameGenerator->SetDirectory( argv[1] );

	//Read DICOM files
	try
	{
		std::cout << std::endl << "The directory: " << std::endl;
		std::cout << std::endl << argv[1] << std::endl << std::endl;
		std::cout << "Contains the following DICOM Series: ";
		std::cout << std::endl << std::endl;

		typedef std::vector< std::string > SeriesIdContainer;

		const SeriesIdContainer & seriesUID = nameGenerator->GetSeriesUIDs();

		SeriesIdContainer::const_iterator seriesItr = seriesUID.begin();
		SeriesIdContainer::const_iterator seriesEnd = seriesUID.end();

		while( seriesItr != seriesEnd )
		{
			std::cout << seriesItr->c_str() << std::endl;
			++seriesItr;
		}

		std::string seriesIdentifier;
		if( argc > 4 ) // If no optional series identifier
		{
			seriesIdentifier = argv[4];
		}

		else
		{
			seriesIdentifier = seriesUID.begin()->c_str();
		}

		std::cout << std::endl << std::endl;
		std::cout << "Now reading series: " << std::endl << std::endl;
		std::cout << seriesIdentifier << std::endl;
		std::cout << std::endl << std::endl;

		typedef std::vector< std::string > FileNamesContainer;
		FileNamesContainer fileNames;

		//Set file names
		fileNames = nameGenerator->GetFileNames( seriesIdentifier );
		reader->SetFileNames( fileNames );

		//Subtract images
		typedef itk::SubtractImageFilter 
		SubtractImageFilterType;

		SubtractImageFilterType::Pointer subtractFilter = SubtractImageFilterType::New ();

		subtractFilter->SetInput1(image1);
		subtractFilter->SetInput2(image2);
		subtractFilter->Update();

		//Update reader
		try
		{
			reader->Update();
		}
		//Catch errors
		catch (itk::ExceptionObject &ex)
		{
			std::cout << ex << std::endl;
			return EXIT_FAILURE;
		} 
	}
	catch (itk::ExceptionObject &ex)
	{
		std::cout << ex << std::endl;
		return EXIT_FAILURE;
	} 
	return EXIT_SUCCESS;
}

Include a make file similar to:

CMakeLists.txt

cmake_minimum_required(VERSION 2.8)
 
project(materialDecomposition)
 
find_package(ITK REQUIRED)
include(${ITK_USE_FILE})
 
add_executable(materialDecomposition MACOSX_BUNDLE materialDecomposition.cxx)
target_link_libraries(SubtractImageFilter ${ITK_LIBRARIES})